Решение игр в чистых стратегиях — киберпедия
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНЫМ РАБОТАМ
по дисциплине
“Теория принятия решений”
для студентов направления подготовки
09.03.02 «Информационные системы и технологии»
Рассмотрено на заседании кафедры «Автоматизированные системы управления»
Протокол №
от __ _________ 2022 г.
Утверждено на заседании
учебно-издательского совета ДОННТУ
протокол № __от «__» _________ 20__г.
Донецк
УДК 004.942
Методические указания к лабораторным работам по дисциплине ” Теория принятия решений ” для студентов направления подготовки 09.03.02 «Информационные системы и технологии» / сост.: Е. О. Савкова, Е. А. Шуватова. – Донецк : ДОННТУ, 2022. – 52 с.
В методических указаниях представлены теоретические сведения, методические рекомендации и задания для выполнения лабораторных работ по дисциплине ” Теория принятия решений “.
Методические указания к лабораторным работам предназначены для студентов направления подготовки 09.03.02 «Информационные системы и технологии» профиль «Информационные системы и технологии в технике и бизнесе» очной формы обучения.
Утверждено методической комиссией направления 09.03.02 «Информационные системы и технологии».
Составители: к.т.н., доц., доц. каф. АCУ Савкова Е.О.
асс. каф. АСУ Шуватова Е.А.
Рецензенты:
Ответственный за выпуск: зав. каф. АСУ Привалов М.В.
СОДЕРЖАНИЕ
Лабораторная работа № 1. 4
Лабораторная работа №2. 11
Лабораторная работа №3. 19
Лабораторная работа №4. 20
Лабораторная работа №5. 31
Лабораторная работа №6. 43
Лабораторная работа №7. 54
Лабораторная работа №8. 55
Лабораторная работа № 1
Тема:Принятие решений в условиях риска.
Задание:С помощью дерева решений решить задачу согласно варианту.
Задачи
1. Вас пригласили на телевизионную игру Колесо фортуны. Колесо управляется электронным образом с помощью двух кнопок, которые сообщают колесу сильное (В) или слабое (Н) вращение. Само колесо разделено на равные области — белую (Б) и красную (К). Вам сообщили, что в белой области колесо останавливается с вероятностью 0,3, а в красной — 0,7. Плата, которую вы получаете за игру, равна (в долл.) следующему.
Изобразите соответствующее дерево решений.
2. Фермер Мак-Кой может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0,25, 0,30 и 0,45. Если цены возрастут, урожай кукурузы даст 30 000 долл. чистого дохода, а урожай соевых бобов — 10 000 долл. Если цены останутся неизменными, Мак-Кой лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 35 000 и 5 000 долл. соответственно.
а) Представьте данную задачу в виде дерева решений.
б) Какую культуру следует выращивать Мак-Кою?
3. Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может измениться в зависимости от условий рынка. Существует 10% -ная вероятность, что ситуация на рынке ценных бумаг ухудшится, 50%-ная — что рынок останется умеренным и 40%-ная — рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиции при трех возможностях развития рынка.
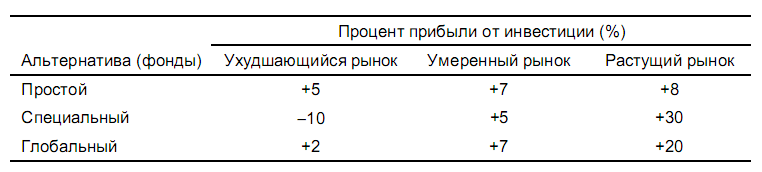
а) Представьте задачу в виде дерева решений.
б) Какой фонд открытого типа вам следует выбрать?
4.Сергей выбирает спортивную секцию, руководствуясь стоимостью абонента и затратами на инвентарь и спортивное снаряжение. У него есть следующие варианты: волейбол, теннис или фехтование.
| Критерии Спорт. | Единовременные затраты руб. | Стоимость месячного абонемента, руб. |
| Волейбол | ||
| Фехтование | ||
| Теннис |
Через месяц с вероятностью 0,2 (волейбол); 0,5 (теннис) и 0,3 (фехтование) его могут отчислить из секции за несоответствие требованием и он может выбрать другую секцию. Используя дерево решений, определите, какую следует выбрать секцию, чтобы затраты были минимальными и Сергей продолжал заниматься спортом в течении года.
5. Предположим, у вас имеется возможность вложить деньги либо в 7,5%- ные облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8%, и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда — на 20% . Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% — наступление спада. Ваше решение относительно инвестиций принимается с учетом экономических условий следующего года.
а) Представьте задачу в виде дерева решений.
б) Будете ли вы покупать акции фонда или облигации?
6. Садовник решает что посадить в саду. У него есть варианты: яблоня, вишня или яблоню и вишню пополам.
| Критерии Саженец | Покупка саженцев Тыс. руб. | Прибыль, тыс. руб. | |
| Нормальная погода | Засуха, вер. 0.3 | ||
| Яблоня | |||
| Вишня |
Используя дерево решений, определите, что следует сажать, чтобы через два года получить максимальный доход.
7. Фирма планирует производство новой продукции быстрого питания в национальном масштабе. Исследовательский отдел убежден в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирмы. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдется в 100 000 долл., а в случае успеха принесет 950000 долл. годового дохода. В случае провала рекламной кампании (вероятность этого составляет 30%) годовой доход оценивается лишь в 200 000 долл. Если рекламная кампания не проводится вовсе, годовой доход оценивается в 400000 долл. при условии, что покупателям понравится новая продукция (вероятность этого равна 0,8), и в 200000долл. с вероятностью 0,2, если покупатели останутся равнодушными к новой продукции.
а) Постройте соответствующее дерево решений.
б)Как должна поступить фирма в связи с производством новой продукции?
8. Симметричная монета подбрасывается три раза. Вы получаете один доллар за каждое выпадение герба (Г) и дополнительно 0,25 доллара за каждые два последовательных выпадения герба (заметим, что выпадение ГГГ состоит из двух последовательностей ГГ). Однако вам приходится платить 1,1 долл. за каждое выпадение решки (Р). Вашим решением является участие или неучастие в игре.
а) Постройте соответствующее дерево решений для описанной игры.
б) Будете ли вы играть в эту игру?
9. Садовник решает что посадить в саду. У него есть варианты: яблоня, вишня, груша или два разных дерева поровну.
| Критерии Саженец | Покупка саженцев Тыс. руб. | Прибыль, тыс. руб. | ||
| Нормальная погода | Дождь вер 0,2 | Засуха, вер. 0.3 | ||
| Яблоня | ||||
| Вишня | ||||
| Груша |
Найдите оптимальное решение, чтобы через два года получить максимальный доход.
10. Предположим, у вас имеется возможность сыграть в игру следующего содержания. Симметричная игральная кость бросается два раза, при этом возможны четыре исхода: 1) выпадает два четных числа, 2) выпадает два нечетных числа, 3) выпадает сначала четное, затем нечетное число, 4) выпадает сначала нечетное, затем четное число. Вы можете делать одинаковые ставки на два исхода. Например, вы можете поставить на два четных числа (исход 1) и два нечетных (исход 2). Выигрыш на каждый доллар, поставленный на первый исход, равен 2 доллара, на второй и третий исходы — 1,95 доллара, на четвертый — 1,50 доллара.
а) Постройте дерево решений для описанной игры.
б) На какие исходы следует делать ставки?
в) Можно ли иметь стабильный выигрыш в этой игре?
11. Фирма производит партии продукции с 0,8, 1, 1,2 и 1,4 % бракованных изделий с вероятностями 0,4, 0,3, 0,25 и 0,05 соответственно. Три потребителя А, В и С заключили контракт на получение партий изделий с процентом некачественных изделий не выше 0,8, 1,2 и 1,4 % соответственно. Фирма штрафуется в сумме 1000 долл. за каждый пункт процента (пункт процента — это одна десятая процента) в случае, если процент некачественных изделий выше указанного. Наоборот, поставка партий изделий с меньшим процентом бракованных изделий, чем оговорено в контракте, приносит фирме прибыль в 500 долл. за каждый пункт процента. Предполагается, что партии изделий перед отправкой не проверяются.
а) Постройте соответствующее дерево решений.
б) Какой из потребителей должен иметь наивысший приоритет при получении своего заказа?
12. Фирма планирует открыть новое предприятие в Арканзасе. В настоящее время имеется возможность построить либо крупное предприятие, либо небольшое, которое через два года можно будет расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на десятилетний период. Фирма оценивает, что на протяжении этих 10 лет вероятность высокого и низкого спроса на производимую продукцию будет равна 0,75 и 0,25 соответственно. Стоимость немедленного строительства крупного предприятия равна 5 млн. долл., а небольшого — 1 млн. долл. Расширение малого предприятия через два года обойдется фирме в 4,2 млн. долл. Прибыль, получаемая от функционирования производственных мощностей на протяжении 10 лет, приводится в следующей таблице.
а) Постройте соответствующее дерево решений, принимая во внимание, что через два года фирма может либо расширить небольшое предприятие, либо не расширять его.
б) Сформулируйте стратегию строительства для фирмы на планируемый 10летний период. (Для простоты не принимайте во внимание возможную инфляцию.)
13. Электроэнергетическая компания использует парк из 20 грузовых автомобилей для обслуживания электрической сети. Компания планирует периодический профилактический ремонт автомобилей. Вероятность поломки автомобиля в первый месяц равна нулю, во второй месяц — 0,03 и увеличивается на 0,01 для каждого последующего месяца, по десятый включительно. Начиная с одиннадцатого месяца и далее, вероятность поломки сохраняется постоянной на уровне 0,13. Случайная поломка одного грузового автомобиля обходится компании в 200 долл., а планируемый профилактический ремонт в 75 долл.
Компания хочет определить оптимальный период (в месяцах) между планируемыми профилактическими ремонтами.
а) Постройте соответствующее дерево решений.
б) Определите оптимальную длину цикла для профилактического ремонта.
14. В магазине проводится акция: продажа елочных гирлянд оптом. Упаковки гирлянд трех видов каждая стоимостью 100 руб.:
20 упаковок 1 вида, в каждой: 10 красных, 15 синих и 5 зеленых;
24 упаковки 2 вида, в каждой: 7 красных, 5 синих, 18 зеленых;
16 упаковок 3 вида, в каждой: 12 красных, 8 синих, 10 зеленых.
Покупателю необходимо 20 красных гирлянд. Сколько нужно купить упаковок, если упаковки одинаковые и их нельзя вскрывать? Решите задачу с помощью дерева решений.
15. Рассматриваются три проекта относительно инвестирования: А, В, С. По прогнозам аналитиков в будущем возможен один из трех вариантов развития экономики (три состояния экономики) с вероятностями: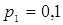
,
, 
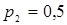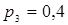. В зависимости от состояния экономики возможны такие значения чистой теперешней стоимости(NPV) этих проектов (в тыс. грн.):
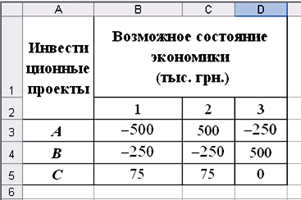
Необходимо сравнить привлекательность этих проектов для инвестирования по показателям количественной оценки эффективности риска.
16. Начальник ДОКа, в настоящее время выпускающего продукцию X1 в текущем объеме V1тек = 1000 ед., считает, что расширяется рынок продукции Х2. Были проведены маркетинговые исследования, определившие вилки спроса на продукцию и Х2 (V1max = 1000 ед.; V1min = 5000 ед.; V2max = 8000 ед.; V2min = 4000 ед.) и вероятности высокого и низкого спроса (D1max = 0,7; D1min = 1 -D1max = 0,3; D2max = 0,6; D2min = 1-D2max = 0,4). Установлено, что даже минимальный спрос намного превышает действующие мощности ДОКа, которые могут быть использованы для производства продукции обоих видов. Известна прибыль на единицу продукции каждого вида (P1 = 1 д.е.; Р2 = 0,9 д.е.). Рассчитаны затраты (К = = 0,4 • 103 д.е.) на удвоение мощности ДОКа (для параллельного производства продукции в текущем объеме и продукции Х2 в эквивалентном количестве) V1тек = 1000 ед. и V2экв = 900 ед., на увеличение мощности комбината под максимальный и минимальный спрос на текущую продукцию (K1max = 2 • 103 д.е. и K1min= = 1,4 • 103 д.е.) и под максимальный и минимальный спрос на продукцию Х2 (соответственно К1max = 1,2 • 103 д.е. и К2тiп = 0,8 • 103 д.е.).
Определить целесообразность замены продукции и развития мощностей, в том числе под одновременный выпуск продукции.
17. Некоторое предприятие владеем акциями стоимостью 1000 у.е. Существует три множества решений: дополнительно купить акции на сумму 500 у.е (А), держать акции (Б), продать их (В). Вероятность 20% роста курса акции составляет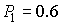 
, а вероятность снижения курсовой стоимости – 
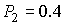. Какие решения необходимо принять, чтобы максимизировать ожидаемую прибыль?
18. Руководство компании решает реконструировать фабрику — химчистки по одному из трех проектов. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка
| Номер стратегии | Действия компании | Выигрыши, усл. руб., при состоянии экономической среды |
| благоприятному | неблагоприятному | |
| По 1-му проекту | – 80000 | |
| По 2-му проекту | – 150000 | |
| По 3-му проекту | – 40000 |
Известно, что фирма, проводящая дополнительные исследования, способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка представлены в табл. 3.5.
| Прогноз фирмы | Фактически | |
| благоприятный | неблагоприятный | |
| Благоприятный | 0,81 | 0,19 |
| Неблагоприятный | 0,23 | 0,77 |
Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,81 этот прогноз оправдывается (с вероятностью 0,19 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,77.
Компания заказала фирме прогноз состояния рынка и фирма утверждает, что ситуация будет благоприятной с вероятностью 0,42 и ситуация будет неблагоприятной с вероятностью 0,58
Определить оптимальное решение
Лабораторная работа №2
Тема: Решение задач в условиях риска
Цель: Приобрести навыки поиска рациональных решений с помощью критериев Байеса, Лапласа, Гермейера и Ходжа-Лемана.
Порядок выполнения работы:
1. Самостоятельно определить вероятности случайных событий.
2. Решить задачу всеми предлагаемыми методами.
3. Сравнить результаты.
4. Определить уровень оптимизма, если ЛПР считает, что самое рациональное решение – это альтернатива А2.
Варианты заданий:
1.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -1 | |||
| А2 | -1 | ||||
| А3 | -2 | ||||
| А4 | -1 | -2 | -1 | ||
| А5 | -1 |
2.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -5 | |||
| А2 | -3 | -4 | -9 | -2 | |
| А3 | -8 | -9 | |||
| А4 | -2 | -9 | |||
| А5 | -7 |
3.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -5 | -2 | -2 | ||
| А2 | -2 | ||||
| А3 | |||||
| А4 | -2 | ||||
| А5 | -1 |
4.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -4 | |||
| А2 | -2 | -2 | |||
| А3 | -1 | ||||
| А4 | -2 | ||||
| А5 | -3 | -5 |
5.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -3 | ||||
| А4 | -3 | ||||
| А5 | -6 |
6.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -6 | ||||
| А3 | |||||
| А4 | -2 | ||||
| А5 | -5 | -5 |
7.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | -2 | -1 | ||
| А3 | |||||
| А4 | -4 | ||||
| А5 |
8.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | ||||
| А3 | |||||
| А4 | |||||
| А5 | -1 | -5 |
9.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | |||||
| А5 | -1 | -2 | -3 | -4 | -5 |
10.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -4 | ||||
| А3 | -1 | ||||
| А4 | |||||
| А5 | -4 |
11.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -2 | ||||
| А2 | |||||
| А3 | -1 | -2 | |||
| А4 | -4 | ||||
| А5 |
12.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -7 | ||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | -5 | -2 | |||
| А5 | -2 |
13.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | -5 | |||
| А4 | -4 | ||||
| А5 | -1 |
14.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -1 | ||||
| А2 | |||||
| А3 | |||||
| А4 | -3 | -3 | |||
| А5 |
15.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -6 | ||||
| А2 | |||||
| А3 | |||||
| А4 | -1 | -4 | |||
| А5 | -1 |
16.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -3 | ||||
| А4 | |||||
| А5 | -5 |
17.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -5 | ||||
| А2 | |||||
| А3 | |||||
| А4 | |||||
| А5 |
18.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -6 | ||||
| А2 | |||||
| А3 | -7 | ||||
| А4 | |||||
| А5 | -5 |
19.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | ||||
| А3 | -5 | ||||
| А4 | |||||
| А5 | -7 |
20.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -2 | ||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | -1 | ||||
| А5 | -2 |
21.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -4 | ||||
| А3 | |||||
| А4 | -5 | -2 | |||
| А5 |
22.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -5 | ||||
| А3 | |||||
| А4 | -1 | ||||
| А5 | -3 |
23.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 | -1 | ||||
| А5 |
24.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -4 | ||||
| А4 | -1 | ||||
| А5 |
25.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | |||||
| А5 | -5 |
Лабораторная работа №3
Лабораторная работа №4.
Тема: Решение однокритериальной статической задачи в условиях определенности
Задание
Придумайте собственную задачу разработки управленческого решения, которая может быть решена с использованием методов математического программирования. Используйте одну из возможных ее постановок – задача распределения ресурсов, задача о назначениях и т.п. Обеспечьте задание реальных (на основе справочных данных, или данных, полученных в результате проведения дополнительных специальных исследований) значений неконтролируемых параметров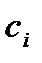 
и 
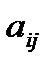. Задайтесь значениями ограничений 
.
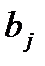Порядок выполнения работы
Составьте краткое описание предприятия, в интересах которого решается задача и опишите проблему, которая должна быть разрешена.
Сформулируйте цель разрешения проблемы.
Сформулируйте критерий, который должен использоваться при решении задачи.
Опишите способ, которым были получены неконтролируемые параметры задачи.
Сделайте математическую запись задачи
Минимум остатков ресурсов
Максимум прибыли
Запрограммируйте задачу средствами Excel и решите ее. Получите отчеты по результатам, пределам и устойчивости и проанализируйте их.
Пример содержания отчета по лабораторной работе №2 «Решение однокритериальной статической задачи в условиях определенности»
1. Исходные данные:
Предприятие выпускает восемь видов товаров, реализуемых по известным ценам (таблица П1). Для производства указанных товаров используется 15 видов ресурсов (таблица П2). Рассматривалась проблема недостаточности дохода предприятия. Целью решения задачи является определение такого количество товаров каждого вида, которое максимизировало бы доход предприятия. Поэтому в качестве критерия рассматривается величина дохода от реализации все произведенной продукции.
2. Решение:
Задача представляет собой разновидность производственной задачи или задачи распределения ресурсов. В рассматриваемом примере неконтролируемые параметры были выбраны случайным способом. Математическая запись задачи имеет вид:
.
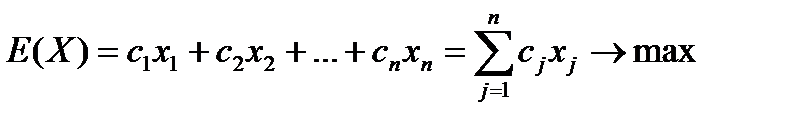При этом:
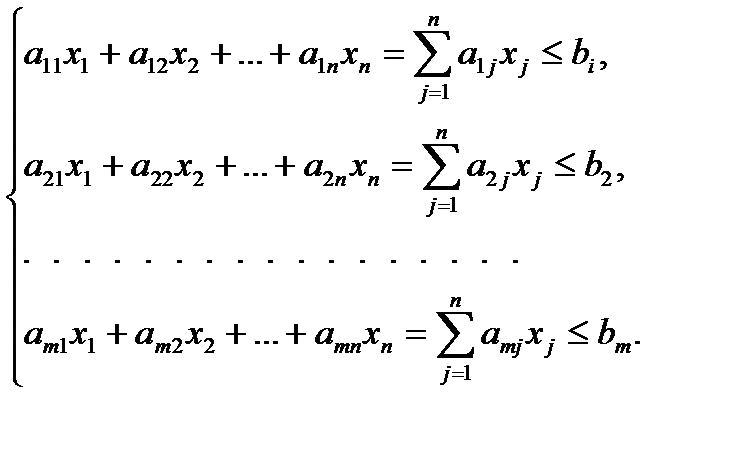
Это для критерия максимум прибыли.
С помощью Excel исходные данные оформлены в виде таблиц П1 и П2:
Таблица П1. Выпускаемая продукция
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход |
| Количество (шт.) | |||||||||
| Цена (руб.) |
Таблица П2. Ресурсы
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | <= | ||||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | <= | |||||
| Ресурс 3 (ед. измерения) | <= | ||||||||||
| Ресурс 4 (ед. измерения) | <= | ||||||||||
| Ресурс 5 (ед. измерения) | <= | ||||||||||
| Ресурс 6 (ед. измерения) | <= | ||||||||||
| Ресурс 7 (ед. измерения) | <= | ||||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | <= | |||
| Ресурс 9 (ед. измерения) | <= | ||||||||||
| Ресурс 10 (ед. измерения) | <= | ||||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | <= | ||
| Ресурс 12 (ед. измерения) | <= | ||||||||||
| Ресурс 13 (ед. измерения) | <= | ||||||||||
| Ресурс 14 (ед. измерения) | <= | ||||||||||
| Ресурс 15 (ед. измерения) | <= |
С помощью функции СУММПРОИЗВ() в ячейке Доход рассчитана величина дохода (таблица П1), а также расход ресурсов (таблица П2) (первоначально они равны нулю, поскольку вектор количества товара еще не подобран).
После выполнения программы надстройки Поиск решения, где в качестве целевой функции была задана ячейка Доход, в качестве изменяемых параметров ячейки Количество (таблица П1), добавлены ограничения, а также во вкладке Параметры был установлен флажок Линейная модель в результате расчетов получаем:
Таблица П3. Оптимальный выпуск продукции
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход |
| Количество (шт.) | 13,93127 | 3,200906 | 5,386733 | 0,599527 | 20,1504 | ||||
| Цена (руб.) | 1034,812 |
При этом ресурсы расходуются в следующем количестве:
Таблица П4. Расход ресурсов на выпуск продукции
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | <= | ||||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 13,69 | <= | ||||
| Ресурс 3 (ед. измерения) | 546,25 | <= | |||||||||
| Ресурс 4 (ед. измерения) | <= | ||||||||||
| Ресурс 5 (ед. измерения) | 31,73 | <= | |||||||||
| Ресурс 6 (ед. измерения) | <= | ||||||||||
| Ресурс 7 (ед. измерения) | 351,68 | <= | |||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 9,12 | <= | ||
| Ресурс 9 (ед. измерения) | 368,90 | <= | |||||||||
| Ресурс 10 (ед. измерения) | 620,80 | <= | |||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 9,90 | <= | |
| Ресурс 12 (ед. измерения) | <= | ||||||||||
| Ресурс 13 (ед. измерения) | 669,27 | <= | |||||||||
| Ресурс 14 (ед. измерения) | 69,20 | <= | |||||||||
| Ресурс 15 (ед. измерения) | <= |
При решении задачи средствами пакета Excel сформированы отчеты по результатам, по устойчивости и по пределам.
Отчет по результатам (Таблица П5) содержит начальные (Исходно) и конечные (Результат) значения целевой функции и изменяемых ячеек, а также сводку результатов использования ресурсов. В столбце Статус символами связанное или несвязанное обозначены соответственно полное или неполное использование соответствующего ресурса. В рассматриваемом примере полностью израсходованы Ресурс 1,4,6,12,15. Установлено, что следует обратить внимание на нерациональное управление запасами ресурсов 2,5,8,11 и 14, которые заказываются в гораздо большем количестве, чем требуется для производства продукции.
Таблица П5. Отчет по результатам
| Microsoft Excel 11.0 Отчет по результатам | ||||||
| Рабочий лист: [Книга1]Лист1 | ||||||
| Отчет создан: 24.01.2008 15:13:45 | ||||||
| Целевая ячейка (Максимум) | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| R3C10 | цена доход | 1034,81178 | ||||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| R2C2 | количество товар 1 | 13,93127316 |
§
Общим методом нахождения решения игры любой конечной размерности является ее сведение к задаче линейного программирования. Из основного положения теории игр следует, что при использовании смешанных стратегий такое оптимальное решение всегда существует и цена игры γ находится между верхним и нижним значениями игры (α≤γ≤β).
Допустим, что смешанная стратегия игрока А складывается из стратегий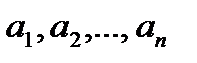 
с вероятностями 
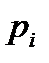(некоторые из значений вероятностей могут быть равны нулю). Оптимальная смешанная стратегия игрока В складывается из стратегий 
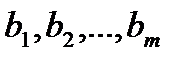с вероятностями 
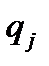. Условия игры определяются платежной матрицей 
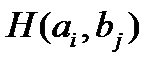с элементами 
, 
; 
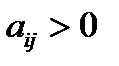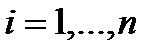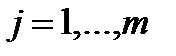. Если игрок А применяет оптимальную смешанную стратегию, а игрок B — чистую стратегию 
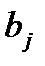, то средний выигрыш игрока А (математическое ожидание выигрыша) составит
.
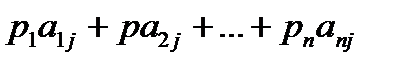Игрок А стремится к тому, чтобы при любой стратегии игрока В его выигрыш был не меньше, чем цена игры γ, а сама цена игры была максимальной. Такое поведение игрока А описывается следующей задачей линейного программирования:
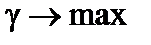(игрок А стремится максимизировать свой выигрыш)
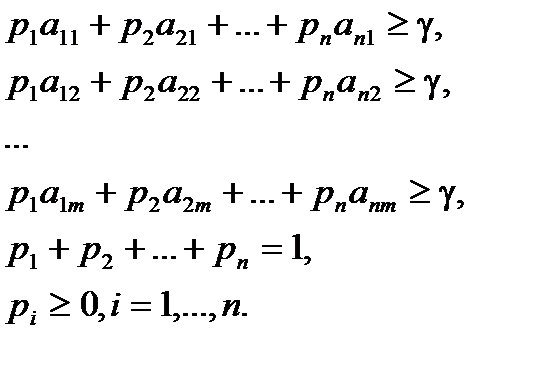
Используя обозначения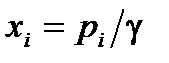 
и соотношение 
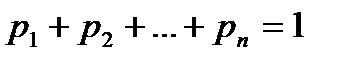, получим 
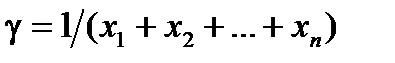. Отсюда
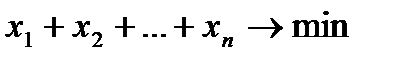
Эта задача всегда имеет решение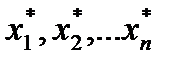 
, получив которое (например, с помощью надстройки Поиск решения MS Excel) можно найти цену игры 
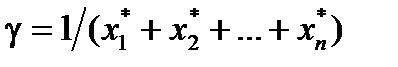и оптимальные значения вероятностей 
— оптимальную смешанную стратегию игрока А.
Требуется обратить внимание на то, что матрица игры представлена в неравенствах в транспонированном виде.
Поведению игрока B соответствует двойственная задача линейного программирования:
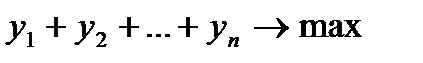
(эквивалентно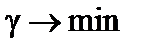 
: игрок B стремится минимизировать свой средний проигрыш)
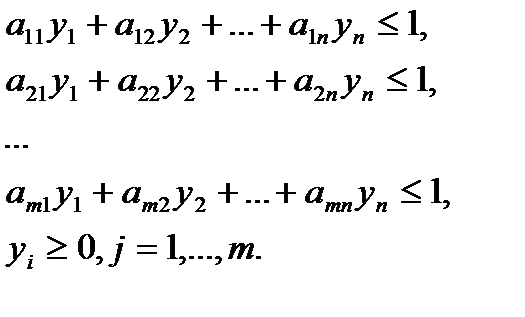
Здесь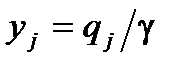 
.
Если в исходной платежной матрице имеется хотя бы один неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование к матрице, все элементы которой строго положительны. Для этого достаточно увеличить все элементы исходной матрицы на одно и то же число
, 
.
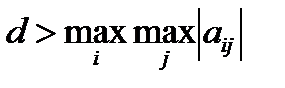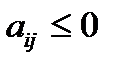При таком преобразовании матрицы оптимальные стратегии игроков не изменятся. Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры, γ нужно уменьшить на d.
Варианты заданий:
1.
2.
| В1 | В2 | В3 | В4 | |
| А1 | -2 | -3 | ||
| А2 | ||||
| А3 | -2 | |||
| А4 |
3.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | -3 | -2 | ||
| А3 | -4 | -1 | ||
| А4 | -3 |
4.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | -1 | |||
| А3 | -3 | |||
| А4 | -3 | -1 |
5.
| В1 | В2 | В3 | В4 | |
| А1 | -1 | |||
| А2 | ||||
| А3 | ||||
| А4 | -3 |
6.
| В1 | В2 | В3 | В4 | |
| А1 | -1 | |||
| А2 | -5 | |||
| А3 | ||||
| А4 |
7.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | -1 |
8.
9.
| В1 | В2 | В3 | В4 | |
| А1 | -4 | -5 | ||
| А2 | -3 | -4 | -9 | -2 |
| А3 | -8 | -9 | ||
| А4 | -9 |
10.
| В1 | В2 | В3 | В4 | |
| А1 | 0,8 | 0,6 | 0,2 | -0,8 |
| А2 | -0,8 | 0,9 | -0,4 | 0,5 |
| А3 | 1,7 | 0,5 | 0,3 | 0,6 |
| А4 | 0,3 | -0,8 | 0,1 | 0,7 |
11.
| В1 | В2 | В3 | В4 | |
| А1 | -5 | -1 | ||
| А2 | ||||
| А3 | -6 | |||
| А4 | -9 | -2 |
12.
| В1 | В2 | В3 | В4 | |
| А1 | -2 | -1 | -2 | |
| А2 | -2 | -5 | ||
| А3 | ||||
| А4 | -2 |
13.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | -2 | -5 | ||
| А3 | -3 | -5 | ||
| А4 |
14.
| В1 | В2 | В3 | В4 | |
| А1 | -8 | |||
| А2 | -1 | |||
| А3 | ||||
| А4 | -3 |
15.
| В1 | В2 | В3 | В4 | |
| А1 | -5 | |||
| А2 | -4 | |||
| А3 | ||||
| А4 |
16.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 | -5 | -2 | -3 | |
| А4 | -2 | -5 |
17.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | -1 | -6 | ||
| А3 | -2 | -8 | ||
| А4 | -2 | -4 |
18.
| В1 | В2 | В3 | В4 | |
| А1 | -7 | |||
| А2 | -2 | -5 | ||
| А3 | ||||
| А4 | -5 |
19.
| В1 | В2 | В3 | В4 | |
| А1 | -5 | |||
| А2 | ||||
| А3 | -8 | -5 | ||
| А4 | -3 |
20.
| В1 | В2 | В3 | В4 | |
| А1 | -7 | |||
| А2 | ||||
| А3 | -3 | |||
| А4 | -3 |
21.
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 | -3 | |||
| А4 | -6 |
22.
| В1 | В2 | В3 | В4 | |
| А1 | -3 | |||
| А2 | ||||
| А3 | ||||
| А4 | -5 |
23.
| В1 | В2 | В3 | В4 | |
| А1 | -5 | -8 | -2 | |
| А2 | -2 | -6 | ||
| А3 | -4 | -3 | -5 | |
| А4 | -1 |
24.
25.
| В1 | В2 | В3 | В4 | |
| А1 | -7 | |||
| А2 | ||||
| А3 | -6 | |||
| А4 |
Лабораторная работа №6
Тема: Итерационный метод решения матричных игр
Цель: Приобрести навыки поиска рациональных решений с помощью итерационного метода.
Порядок выполнения работы:
1. Изучить теоретическую часть;
2. Упростить заданную по варианту матрицу, убрав доминантные строки;
3. С помощью MS Excel или написав программу, определить итерационным методом цену игры и оптимальные стратегии для каждого из игроков.
4. Проверить результат решения с помощью приведения задачи к задаче линейного программирования (ЛП).
Теория:
Ситуации, связанные с принятием решений, в которых два или более разумных противника имеют конфликтующие цели, рассматриваются в теории игр. Само слово «игра» применяется для обозначения некоторого набора правил и соглашений, составляющих данный вид игры, например: футбол, карточная игра, шахматы. Эти ситуации принятия решений отличаются от рассмотренных ранее, где природа, хотя и могла находиться в различных состояниях, но не преследовала каких-либо целей и, следовательно, не рассматривалась в роли соперника.
Общие понятия матричных игр
В игре заинтересованные стороны называются игроками, каждый из которых имеет некоторое множество вариантов выбора (не меньше двух, иначе он фактически не участвует в игре, поскольку заранее известно, что он предпримет). В экономике модель поведения лиц в виде игры возникает, например, при попытке нескольких фирм завоевать наиболее выгодное место на конкурентном рынке, или, например, при желании нескольких лиц (кампаний) разделить некоторое количество продукта (ресурса, финансовых средств) между собой так, чтобы каждому досталось как можно больше. Игроками в конфликтных экономических ситуациях, моделируемых в виде игры, являются производственные и непроизводственные фирмы, банки, отдельные люди и другие экономические агенты. В военных приложениях модель игры используется, например, для наилучшего выбора средств (из имеющихся или потенциально возможных) поражения военных целей противника или защиты от его нападения.
Для игр характерна неопределенность результата. Причины или источники неопределенности относятся к трем группам:
1. Комбинаторные источники (например игра шахматы);
2. Случайные факторы (например игры кости, карточные игры, где случаен расклад);
3. Неопределенность имеет стратегическое происхождение: игрок не знает, какого рода образа действий придерживается его противник. Здесь неопределенность исходит от другого лица.
Далее будем рассматривать игровые модели конфликтов, в которых участвуют два противника, каждый из которых имеет конечное число вариантов выбора решений. С каждой парой решений связан платеж, который один из игроков выплачивает другому (т.е. выигрыш одного игрока равен проигрышу другого). Такие игры принято называть конечными играми двух лиц с нулевой суммой.
В игре принимают участие два игрока: A и B. В распоряжении каждого игрока имеется конечное множество вариантов выбора — стратегий. Пусть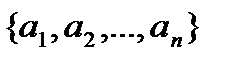 
— множество стратегий игрока A, 
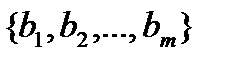— множество стратегий игрока B. С каждой парой стратегий связан платеж, который один из игроков выплачивает другому. Т.е., когда игрок А выбирает стратегию 
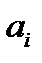(свою i-ю стратегию), а игрок В — стратегию 
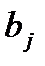, то результатом такого выбора становится платеж 
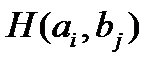. Поскольку стратегий конечное число, то платежи 
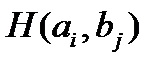образуют матрицу размерности n x m, называемую матрицей платежей (или матрицей игры). Строки этой матрицы соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В.
Пусть два игрока А и В играют в игру, основанную на подбрасывании монеты. Игроки одновременно и независимо друг от друга выбирают герб (Г) или решку (Р). Если результаты двух подбрасываний монеты совпадают (т.е. ГГ или РР), то игрок А получает один доллар от игрока В. Иначе игрок А платит один доллар игроку В.
Для каждого из игроков возможны 2 варианта результатов: выпадения герба или решки, следовательно матрица платежей имеет размерность 2 х 2 следующего вида:
Если результаты двух подбрасываний (т.е. подбрасываний монеты игроками А и В) совпадают, то платеж в 1 доллар получает игрок А. Будем строить матрицу игры, с точки зрения игрока А, т.е. его выигрыши оценивать как положительные, а проигрыши — как отрицательные (с точки зрения В все будет наоборот и мы вполне могли бы построить матрицы платежей, ориентируясь на его точку зрения).
Если результаты подбрасывания различаются, то доллар получает В, значит платеж А равняется –1 доллар. В игре с нулевой суммой выигрыш игрока B равносилен проигрышу игрока A и равен поэтому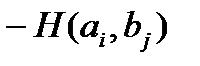 
.
Т.о., мы построили матрицу игры, описывающую заданную ситуацию. Предполагается, что матрица игры обоим игрокам известна.
Исход игры зависит от поведения обоих игроков, которое основывается на выборе правильных стратегий игры, т.е. таких вариантов, при которых так платеж данному игроку будет наибольшим. Однако, в отличие от методов оптимизации, в теории игр игрок не может просто стремиться к максимуму, он вынужден считаться с действиями соперника. Существенно, что ни один из партнеров не знает, какую стратегию применит его противник. Таким образом, имеет место ситуация полной неопределенности, при которой теория вероятности также не может помочь игрокам в выборе решения.
§
Пусть игра задана матрицей A размерности m x n. Каждое разыгрывание игры в чистых стратегиях будет далее называться партией. Метод Брауна-Робинсон — это итеративная процедура построения последовательности пар смешанных стратегий игроков, сходящейся к решению матричной игры.
В 1-ой партии оба игрока выбирают произвольную чистую стратегию. Пусть сыграно k партий, причем выбор стратегии в каждой партии запоминается. В (k 1)-ой партии каждый игрок выбирает ту чистую стратегию, которая максимизирует его ожидаемый выигрыш, если противник играет в соответствии с эмпирическим вероятностным распределением, сформировавшимся за k партий. Оценивается интервал для цены игры и, если он достаточно мал, процесс останавливается. Полученные при этом вероятностные распределения определяют смешанные стратегии игроков.
Достоинства метода Брауна:
1. Этот метод ориентирован на произвольную игру G(m×n).
2. Не требует условия aij>0.
3. Легко реализуем программными методами.
Недостатки метода Брауна: скорость сходимости метода быстро уменьшается с ростом размерности матрицы игры.
Рассмотрим метод на примере игры G(3×3).
| Ai Bj | B1 | B2 | B3 |
| A1 | |||
| A2 | |||
| A3 |
SA=(p1,p2,p3)
SB=(q1,q2,q3)
Строится следующая матрица:
| k | i | B1 | B2 | B3 | j | A1 | A2 | A3 | Vmin | Vmax | V* |
| 0 | 9 | 4.5 | |||||||||
| 9 | 18 | 4.5 | 6.75 | ||||||||
| 11 | 18 | 3.67 | 4.84 | ||||||||
| 11 | 22 | 22 | … | … | … | ||||||
| … | … | … | … | … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | … | … | … | … | … |
где:
k – номер партии.
i – номер стратегии, выбираемой игроком A.
j – номер стратегии, выбираемой игроком В.
Bi– накопленный игроком А выигрыш за k партий, при условии, что в данной партии B выбирает стратегию Bi.
Аj – накопленный игроком В проигрыш за k партий, при условии, что в данной партии A выбирает стратегию Аj.
Vmin – нижняя оценка игры = min (накопленный выигрыш)/k.
Vmax – верхняя оценка игры = max (накопленный проигрыш)/k.
Доказано, что V*=(Vmin Vmix)/2,
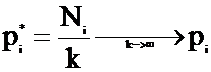
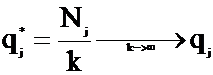
Ni – сколько раз выбирается Аi стратегия.
Nj – сколько раз выбирается Bj стратегия.
Итерационный процесс метода Брауна-Робинсон не является, вообще говоря, монотонным. Кроме того, скорость сходимости метода быстро уменьшается с ростом размерности матрицы игры. Однако он обладает одним неоспоримым преимуществом, которое заключается в исключительной простоте программирования метода.
Варианты заданий:
1.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -1 | |||
| А2 | -1 | ||||
| А3 | -2 | ||||
| А4 | -1 | -2 | -1 | ||
| А5 | -1 |
2.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -5 | |||
| А2 | -3 | -4 | -9 | -2 | |
| А3 | -8 | -9 | |||
| А4 | -2 | -9 | |||
| А5 | -7 |
3.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -5 | -2 | -2 | ||
| А2 | -2 | ||||
| А3 | |||||
| А4 | -2 | ||||
| А5 | -1 |
4.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -3 | -4 | |||
| А2 | -2 | -2 | |||
| А3 | -1 | ||||
| А4 | -2 | ||||
| А5 | -3 | -5 |
5.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -3 | ||||
| А4 | -3 | ||||
| А5 | -6 |
6.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -6 | ||||
| А3 | |||||
| А4 | -2 | ||||
| А5 | -5 | -5 |
7.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | -2 | -1 | ||
| А3 | |||||
| А4 | -4 | ||||
| А5 |
8.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | ||||
| А3 | |||||
| А4 | |||||
| А5 | -1 | -5 |
9.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | |||||
| А5 | -1 | -2 | -3 | -4 | -5 |
10.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -4 | ||||
| А3 | -1 | ||||
| А4 | |||||
| А5 | -4 |
11.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -2 | ||||
| А2 | |||||
| А3 | -1 | -2 | |||
| А4 | -4 | ||||
| А5 |
12.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -7 | ||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | -5 | -2 | |||
| А5 | -2 |
13.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | -5 | |||
| А4 | -4 | ||||
| А5 | -1 |
14.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -1 | ||||
| А2 | |||||
| А3 | |||||
| А4 | -3 | -3 | |||
| А5 |
15.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -6 | ||||
| А2 | |||||
| А3 | |||||
| А4 | -1 | -4 | |||
| А5 | -1 |
16.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -3 | ||||
| А4 | |||||
| А5 | -5 |
17.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -5 | ||||
| А2 | |||||
| А3 | |||||
| А4 | |||||
| А5 |
18.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -6 | ||||
| А2 | |||||
| А3 | -7 | ||||
| А4 | |||||
| А5 | -5 |
19.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -3 | ||||
| А3 | -5 | ||||
| А4 | |||||
| А5 | -7 |
20.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | -2 | ||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | -1 | ||||
| А5 | -2 |
21.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -4 | ||||
| А3 | |||||
| А4 | -5 | -2 | |||
| А5 |
22.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | -5 | ||||
| А3 | |||||
| А4 | -1 | ||||
| А5 | -3 |
23.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 | -1 | ||||
| А5 |
24.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -4 | ||||
| А4 | -1 | ||||
| А5 |
25.
| В1 | В2 | В3 | В4 | В5 | |
| А1 | |||||
| А2 | |||||
| А3 | -2 | ||||
| А4 | |||||
| А5 | -5 |
Лабораторная работа №7
Лабораторная работа №8
Тема:Решение многокритериальной задачи
Задание:решить задачу согласно варианту методом анализа иерархий или методом ранжирования.
Требования к выполнению работы:
1. Нарисовать иерархическую структуру задачи.
2. Определить коэффициенты важности для элементов каждого уровня. Отобразить их на иерархической структуре.
3. Определить согласованность матриц.
4. Рассчитать количественный индикатор качества каждой альтернативы и сделать выводы.
Для метода ранжирования
1. Разбить множество критериев на подмножества для каждой гипотезы.
2. Рассчитать индексы согласия и несогласия.
3. Определить первый уровень индексов согласия и несогласия и выделить первое ядро альтернатив.
4. Продолжить выделение ядер до получения решения.
Варианты заданий
1.Отдел кадров фирмы сузил поиск будущего сотрудника до трех кандидатур: Стив (S), Джейн (J) и Майса(M). Конечный отбор основан на трех критериях: собеседование (С), опыт работы (О) и рекомендации (Р). Отдел кадров использует матрицу А (приведенную ниже) для сравнения трех критериев. После проведенного собеседования с тремя претендентами, сбора данных, относящихся к опыту их работы и рекомендациям, построены матрицы АС, АО и АР. Какого из трех кандидатов следует принять на работу? Оцените согласованность данных.
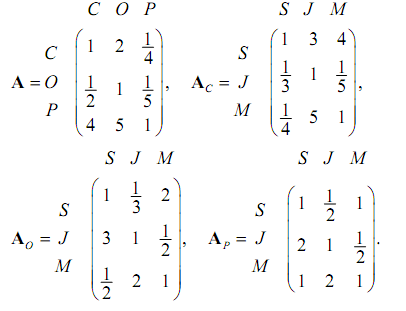
2. Жена и муж выбирают участок для строительства дома. Критериями выбора являются: инфраструктура, время поездки на работу и стоимость. Имеется три участка А, В и С, которые характеризуются следующими параметрами:
| Критерии Участки | Инфраструктура Шкала 1-10 | Стоимость Тыс руб. | Время поездки на работу, мин | |
| Муж | Жена | |||
| А | ||||
| В | ||||
| С |
Определите оптимальный вариант методом анализа иерархий, учитывая, что для жены значимость критериев по убыванию следующая: инфраструктура, время, стоимость, а для мужа: стоимость самый важный критерий, а время и инфраструктура – равнозначны.
Мнение мужа в два раза весомее жены.
3. Кевин и Джун Парки (Kи Д) покупают новый дом. Рассматриваются три варианта — А, В и С. Парки согласовали два критерия для выбора дома: площадь зеленой лужайки (Л) и близость к месту работы (Б), а также разработали матрицы сравнений, приведенные ниже. Необходимо оценить три дома в порядке их приоритета и вычислить коэффициент согласованности каждой матрицы.
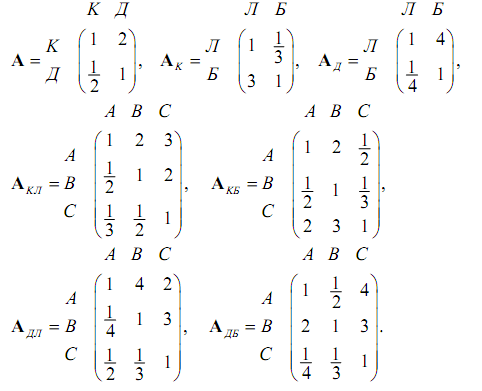
4. Жена и муж выбирают участок для строительства дома. Критериями выбора являются: время поездки на работу, инфраструктура и стоимость. Имеется пять участков А, В, С, D и E которые характеризуются следующими параметрами:
| Критерии Участки | Стоимость Тыс руб. | Инфраструктура Шкала 1-10 | Время поездки на работу, мин | |
| Муж | Жена | |||
| А | ||||
| В | ||||
| С | ||||
| D | ||||
| E |
Определите оптимальный вариант методом ранжирования, если 20 экспертов определили веса критериев следующим образом:
Стоимость – 8;
Расстояние до магазина – 1;
Расстояние до школы – 1;
Время жены – 6;
Время мужа – 4.
5. Школьный совет, районо и родительский комитет решают вопрос об открытии одной из следующих спортивных секций в школе: шахматы, волейбол или шпага. Критериями являются: оплата тренера, количество желающих и стоимость технического обеспечения.
| Критерии Спорт. | Стоимость оборудования Тыс руб. | Оплата тренера, тыс. руб. | Количество желающих |
| Шахматы | |||
| Волейбол | |||
| Шпаги |
Определены девять матриц сравнения для ЛПР на втором иерархическом уровне и определены относительные веса.
| ЛПР | Школьный совет | Районо | Родители | ||||||
| Критерий Секция | С | О | К | С | О | К | С | О | К |
| Шахматы | 0,1 | 0,2 | 0,3 | 0,3 | 0,5 | 0,2 | 0,7 | 0,1 | 0,3 |
| Волейбол | 0,5 | 0,4 | 0,2 | 0,4 | 0,2 | 0,4 | 0,1 | 0,4 | 0,2 |
| Шпаги | 0,4 | 0,4 | 0,5 | 0,3 | 0,3 | 0,4 | 0,2 | 0,5 | 0,5 |
Определите оптимальный вариант методом анализа иерархий, учитывая, что для школьного совета значимость критериев по убыванию следующая: стоимость оборудования, количество желающих, оплата тренеру; для родительского комитета: количество желающих, оплата тренеру, стоимость оборудования; для районо: стоимость оборудования и оплата тренеру равнозначны, но важнее количества желающих.
При вынесении окончательного решения мнение школьного совета, районо и родителей учитываются в соотношении 2:3:1.
6. Автор книги по исследованию операций определил три критерия для выбора издательства, которое будет печатать его книгу: процент авторского гонорара (R), уровень маркетинга (M) и размер аванса (A). Издательства H и P проявили интерес к изданию книги. Используя приведенные ниже матрицы сравнения, необходимо дать оценку двум издательствам и оценить согласованность решения.
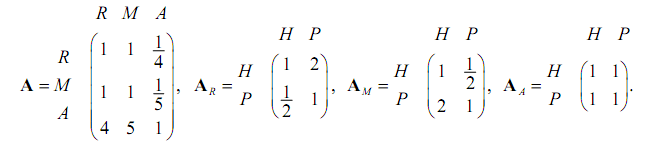
7. Школьный совет решает вопрос об открытии одной из следующих спортивных секций в школе: шахматы, волейбол, спортивная гимнастика, шпага или баскетбол. Критериями являются: оплата тренера, количество желающих, стоимость инвентаря, затраты родителей.
| Критерии Спорт. | Стоимость инвентаря Тыс руб. | Оплата тренера, тыс. руб. | Количество желающих | Затраты родителей, тыс. руб |
| Шахматы | 0,7 | |||
| Волейбол | 2,5 | |||
| Шпаги | ||||
| Баскетбол | 2,5 | |||
| Спортивная гимнастика | 5,5 | 3,5 |
Определите оптимальный вариант методом ранжирования, если 20 экспертов определили веса критериев следующим образом:
Стоимость инвентаря – 8;
Оплата тренера – 6;
Количество желающих – 5;
Затраты родителей – 3;
8. Садовник и хозяин решают вопрос о разбивке сада. Они хотят посадить яблоню или вишню или яблоню и вишню пополам. Критериями выбора являются: затраты на покупку саженцев и будущая прибыль от полученных плодов.
| Критерии Спорт. | Покупка саженцев Тыс. руб. | Прибыль, тыс. руб. |
| Яблоня | ||
| Вишня |
Определите оптимальный вариант методом анализа иерархий, учитывая, что для садовника доход важнее затрат, а для хозяина – наоборот.
При вынесении окончательного решения мнение садовника в 3 раза важнее мнения хозяина.
9. Профессор политологии планирует предсказать исход выборов в местный школьный совет. Кандидаты I, B и S баллотируются на одно место. Профессор делит всех избирателей на три категории: левые (L), центристы (C) и правые (R). Оценка кандидатов основывается на трех факторах: педагогический опыт (О), отношение к детям (Д) и характер (X). Ниже приведены матрицы сравнения для первого иерархического уровня, связанного с градацией избирателей (левые, центристы и правые).
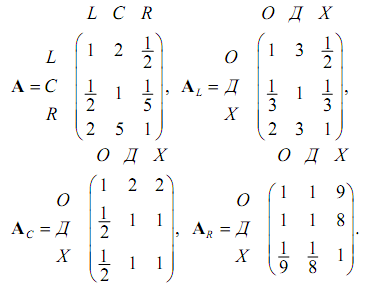
Профессор сгенерировал еще девять матриц сравнения для трех кандидатов на втором иерархическом уровне, связанном с педагогическим опытом, отношением к детям и характером. Затем был использован метод анализа иерархий для сведения этих матриц к следующим относительным весам.
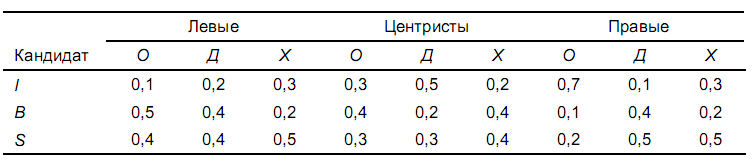
Используя эту информацию, необходимо определить, кто из кандидатов выиграет выборы, и оценить согласованность решения.
10. Брат и сестра выбирают спортивную секцию, руководствуясь стоимостью абонента и затратами на инвентарь и спортивное снаряжение. У них есть следующие варианты: конный спорт, волейбол, теннис или фехтование.
| Критерии Спорт. | Единовременные затраты руб. | Стоимость абонемента, руб. |
| Конный спорт | ||
| Волейбол | ||
| Фехтование | ||
| Теннис |
Определите оптимальный вариант методом анализа иерархий, учитывая, что для сестры важнее покупка снаряжения, чем абонемент, а для брата наоборот.
Сестра и брат должны ходить в одну секцию, но при этом выбор сестры важнее, чем брата в 3 раза.
11.Школьный округ крайне заинтересован в сокращении своих расходов, что вызвано очередным уменьшением бюджетного финансирования начальных школ. Есть две возможности решить эту проблему: ликвидировать программу физического воспитания (Ф) или программу музыкального образования (M). Управляющий округа сформировал комитет с равным представительством от местного школьного совета (С) и ассоциации родителей и учителей (P) для изучения ситуации и выработки предложения. Комитет принял решение изучить ситуацию с точки зрения ограничения бюджета (Б) и потребностей учеников (П). Проведенный анализ дал следующие матрицы сравнения.
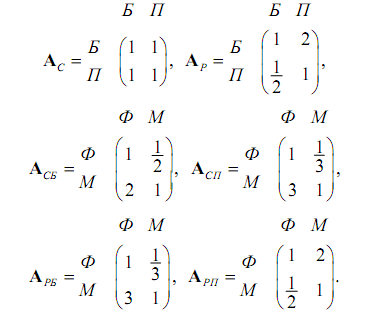
Проанализируйте ситуацию, связанную с принятием решения, и выработайте соответствующее предложение.
12. Решив купить автомобиль, человек сузил свой выбор до трех моделей: М1, М2 и М3. Факторами, влияющими на его решение, являются: стоимость автомобиля (С), стоимость обслуживания (О), стоимость поездки по городу (Г) и сельской местности (М). Следующая таблица содержит необходимые данные, соответствующие трехгодичному сроку эксплуатации автомобиля.
Используйте указанные стоимости для построения матриц сравнений. Оцените согласованность матриц и определите модель автомобиля, которую следует выбрать.
